28 Mar 2019 Identificación de clústers y patrones con QGIS

¿Por qué identificamos patrones?

Patrones, clústers, hotspots, coldspots, distribuciones, agrupaciones, … A menudo, cuando observamos los diferentes elementos contenidos en un mapa o en una capa de información geográfica, nuestro cerebro tiende a intentar identificar ciertos patrones, distribuciones o agrupaciones de entidades que responden a una determinada lógica.

Uno de los posibles motivos de este proceder tiene su explicación en que es precisamente a través de estos patrones que logramos (o ¡creemos lograr!) simplificar y comprender mejor la estructura o la naturaleza de un fenómeno geográfico.

Un patrón o un conjunto de patrones, así como una distribución particular, puede tener su origen y su explicación en la distancia existente entre todos los elementos que conforman la capa de información. Este tipo de patrones pueden ser, por norma general, fácilmente identificables incluso a simple vista. Por el contrario, estas agrupaciones o distribuciones de elementos también pueden tener una explicación de naturaleza estadística. En este caso particular su detección ya no resulta para nada tan simple.

También puede darse el caso, por supuesto, que el origen o explicación de un determinado patrón se deba a la acción combinada de los dos motivos anteriores: la localización y la estadística.

La identificación de patrones puede ser el resultado del proceso de agrupación de entidades que responden a una determinada lógica. Esta tarea puede llevarse a cabo, por ejemplo, mediante un análisis de tipo clúster. También la identificación de hotspots o puntos calientes puede ayudar en esta tarea. A lo largo de este breve artículo, se mostrará como realizar este tipo de análisis a través de QGIS, mediante el uso de diferentes herramientas o complementos.

Para ello, se utilizará un conjunto de datos de los barrios de la ciudad de Barcelona. Este mismo conjunto de datos ya se había utilizado en el artículo sobre la generación de cartogramas con QGIS.

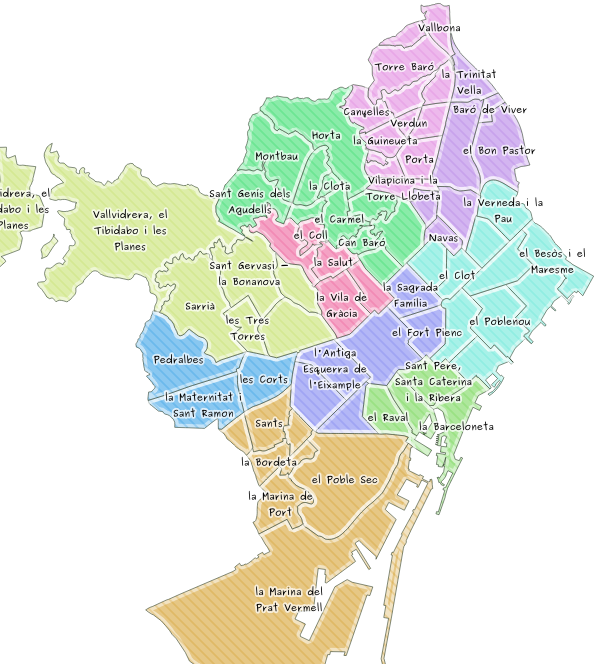
Distribución de los barrios de Barcelona, simbolizados por distritos

La identificación de clústeres utilizando herramientas básicas de QGIS

Un clúster no es más que un conjunto, grupo o cúmulo de entidades agrupadas en base a alguna característica que les resulta común. El ejemplo seguramente más simple de análisis clúster es el basado en la distancia. En este caso, el análisis tendrá por objetivo definir un conjunto de clústeres en función del rango de distancias existente entre los elementos que forman la muestra y que mediante su agrupación deberán conformar cada uno de los clúster.

QGIS dispone de una herramienta básica para llevar a cabo este tipo de análisis. Dentro de la caja de herramientas de procesado, en el apartado de análisis vectorial, se encuentra la herramienta K-means clustering. El uso de esta herramienta es sumamente sencillo. Basta con indicar sobre qué capa se va a trabajar y definir el número de clústeres (p.e. 4) que se desean crear. El resultado se explica por si mismo en la siguiente imagen:

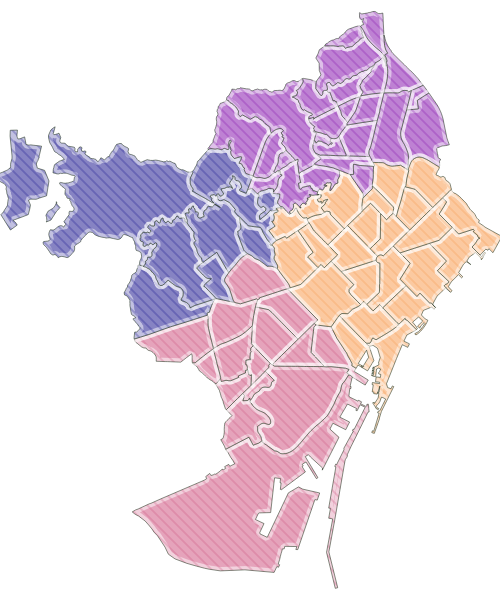
Barrios agrupados en cuatro clústers, basados en la distancia.

El algoritmo K-means clustering organiza o agrupa las entidades de la muestra en el número de clústeres que se haya indicado con anterioridad. Cada entidad de la muestra se asignará al clúster cuyo centroide le resulte más cercano. Si el análisis se basa en entidades de punto, QGIS también ofrece el algoritmo DBSCAN clustering. Este algoritmo posibilita un mayor control para el proceso de asignación a grupos: definir el número máximo de elementos por clúster y la distancia máxima a considerar.

La diferencia básica entre estos dos algoritmos es que el último solo trabaja con entidades de tipo punto, mientras que el primero acepta como capa de entrada puntos, líneas y polígonos. En el caso de líneas y polígonos, utilizará el centroide de cada entidad como elemento de referencia para organizar los distintos clústeres.

La identificación de clústeres utilizando complementos de QGIS

En QGIS 3.x, existe la posibilidad de trabajar con un complemento que permite la definición o, mejor dicho, la identificación de clústeres no en base a un rango de distancias o de proximidad espacial (como en el ejemplo anterior), sino en función de su «proximidad estadística». En otras palabras, permite identificar clústeres con una determinada significación estadística.

El complemento en cuestión lleva por nombre Attribute based clustering. Como su propio desarrollador apunta, este es un complemento que reviste especial interés en aquellos casos en los cuales la localización no es un elemento determinante ni importante para la generación de clústeres. En este caso todo el peso recae en sus características numéricas. El complemento puede instalarse desde el menú Plugin > Manage and Install plugins. Una vez instalado se mostrará como un nuevo icono en la barra de herramientas de los complementos, así como dentro del menú principal Vector.

Aspecto de la barra de herramientas de los complementos de QGIS

Cuando se accede a la ventana de la herramienta Attribute based clustering debe definirse en base a qué atributo o atributos se van a generar los clústeres. Los atributos a utilizar, lógicamente, deberán ser numéricos.

Para obtener los clústeres estadísticos o numéricos deberá indicarse en primer lugar la capa con la que se va a trabajar. Así mismo, será preciso seleccionar los campos o columnas que contienen los valores a analizar. Finalmente, se deberá seleccionar el método de clustering, el número de clústeres (dependiendo del método seleccionado), un valor de umbral, un método aglomerativo/disociativo y el nombre de la columna que almacenará el identificador de clúster.

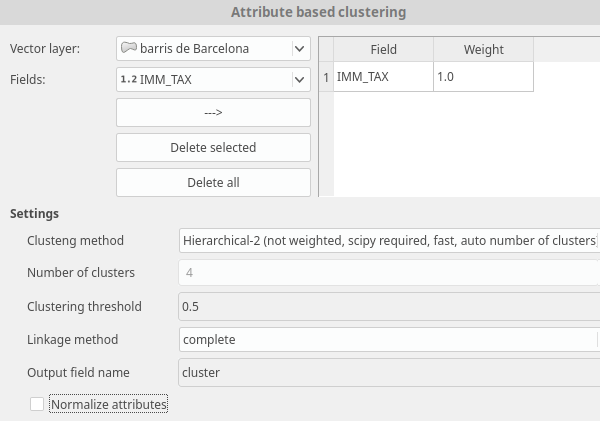
Ventana de la herramienta Attribute based cluster

Los métodos de clustering: K-means o Jerárquico

El método clásico K-means (o K-medias) es un algoritmo de clasificación no supervisado que a grandes rasgos opera del siguiente modo: Inicialmente se seleccionan N elementos de la capa que actuarán como centroides, donde N vendrá definido por el número de clústers que se quieren identificar. A continuación, cada elemento del conjunto de datos se asigna al centroide o clúster que le es más cercano. Seguidamente, se actualiza la posición del centroide inicial en base a la posición de todos los elementos que se han asignado inicialmente al grupo, y se reasignan de nuevo las pertenencias a un determinado clúster. Estos dos últimos procesos (recálculo del centroide y reasignación) irán repitiéndose hasta que se estabilice la muestra y ya no existan cambios en la composición de los clústeres.

Cabe destacar que en este caso concreto, cuando se aplica el algoritmo k-means, el concepto distancia no se aplica desde la perspectiva espacial sino desde la perspectiva numérica.

Como en el caso del método k-means también existe mucha literatura acerca de los análisis clúster jerarquizados. Por ahora, nos limitaremos a apuntar que este método permite clasificar un conjunto de elementos en un número determinado de grupos en base a las semejanzas y discrepancias de los valores numéricos de cada uno de los elementos de la muestra. Resulta especialmente recomendable, en este sentido, hacer una visita al sitio web de GeoDa. Más concretamente, a la documentación relativa al análisis clúster donde se explica de forma muy sencilla los entresijos de estos dos métodos.

Cómo se traduce la teoría a la práctica en QGIS

De vuelta a QGIS, el complemento Attribute based clustering nos ofrece dos tipologías de análisis jerárquico. El primer método es ponderado, lento y en base a un número conocido de clústeres. El segundo es no ponderado, rápido y sin determinar de antemano el número de clústeres existentes.

En el primer resultado que se presenta (en la imagen de la izquierda) se ha realizado un análisis clúster aplicando el método k-means, habiendo definido el número de clústeres a 5. La segunda imagen (derecha) en la que se pueden apreciar ciertos cambios en la organización de los clústeres se ha aplicado el método jerárquico ponderado. En ambos casos, la variable estadística utilizada para definir los clústeres ha sido el valor de la tasa de inmigración por barrios.

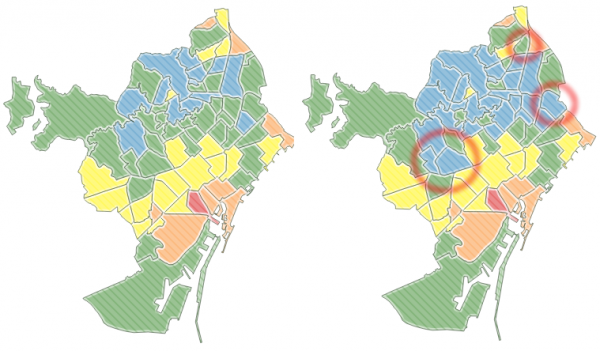
Resultados de la aplicación del método k-means (izquierda) vs jerárquico (derecha)

Se puede comprobar como existe un núcleo de ciertos barrios que pertenecen o se asocian al mismo clúster sea cual sea el método utilizado. En otros casos, hay barrios que se asignan a clústeres distintos en función del método empleado.

Si por contra, utilizando esta misma variable estadística (tasa de inmigración), se lleva a cabo un análisis jerárquico del tipo 2, sin determinar de antemano el número de clústeres a identificar (como sí sucedía en el ejemplo anterior), y definiendo un valor de umbral de 5 puntos con el método simple, se obtiene el siguiente resultado: se identifican, desde un punto de vista estadístico, hasta seis clústeres.

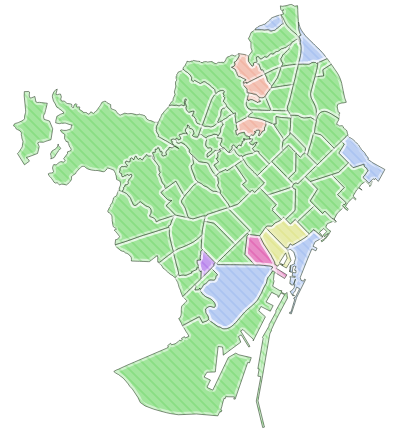
Resultado de un análisis clúster jerárquico del tipo 2

Una particularidad interesante de este complemento de QGIS es que ofrece la posibilidad de realizar agrupaciones de clústeres en base a más de un atributo estadístico. Así, de este modo, pueden identificarse nuevos clústeres basados en los valores relativos a la tasa de inmigración, la renta familiar y la población de cada barrio. Para ello, puede aplicarse un análisis de clústeres de tipo jerárquico, asignando un peso de 0.25 a la variable de la tasa de inmigración, de 0.25 a la renta familiar, y de 0.5 a la población. El resultado obtenido (cuatro clústeres) es el que puede observarse a continuación:

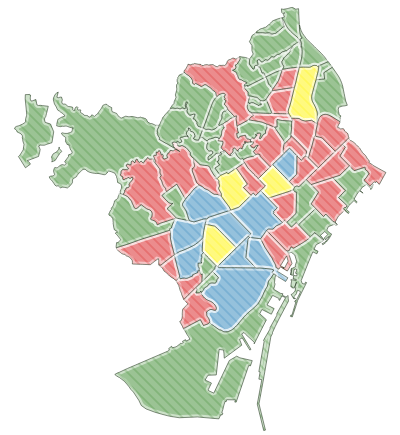
Resultado de un análisis clúster jerárquico multivariable

Cabe recordar que este tipo de agrupación de entidades en clústeres, mediante el complemento Attribute based clustering, está basado en el concepto de similaridad de los valores numéricos de las variables analizadas. Por tanto, estos clústeres no respetan ni guardan relación alguna con el concepto de contigüidad ni de compacidad. Los clústeres identificados son meramente estadísticos.